You cannot select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
|
|
8 years ago | |
|---|---|---|
| doc | 8 years ago | |
| scaling | 8 years ago | |
| tests | 8 years ago | |
| README.md | 8 years ago | |
| setup.py | 8 years ago | |
README.md
scaling
Convert quantities between model and prototype scale using Froude and Reynolds similitude.
Installation
pip install git+http://git.wrl.unsw.edu.au:3000/danh/scaling.git
Usage
>>> from scaling import FroudeConverter
>>> froude = FroudeConverter()
>>> # Convert model value of 200 mm to prototype value (m) with scale of 10
>>> froude.model_to_proto(200, length_scale=10, input_unit='mm', target_unit='m')
2.0
>>> # Get Froude scaling exponent for quantities of time
>>> froude.scaling_exponent('s')
0.5
>>> # Get length, mass and time dimensions for quantities of energy
>>> froude.dimensions('kJ')
'L^2 M^1 T^-2'
Dataframes are also accepted, and specific units can be specified for the values in the index.
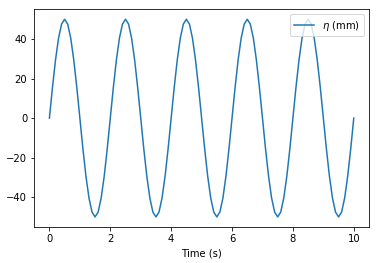
>>> T = 2
>>> H = 100
>>> # Generate regular waves with height=100mm, and period=2s
>>> t = np.arange(0, 10.1, 0.1)
>>> eta = 0.5 * H * np.sin(t * 2 * np.pi / T)
>>> df_model = pd.DataFrame(index=t, data=eta)
>>> df_model.columns = ['$\eta$ (mm)']
>>> df_model.index.name = 'Time (s)'
>>> df_model.plot()
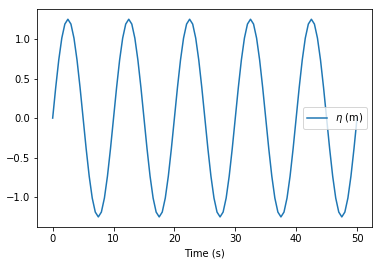
>>> # Convert to prototype dimensions, with length scale=25
>>> df_proto = froude.model_to_proto(
df_model,
length_scale=25,
input_unit='mm',
target_unit='m',
index_input_unit='s',
index_target_unit='s')
>>> df_proto.columns = ['$\eta$ (m)']
>>> df_proto.plot()
scaling uses pint for unit and dimension conversions. pint is able to interpret a wide range of different input units.
>>> # Convert water head model value (mm) to prototype pressure value (kPa)
>>> froude.model_to_proto(10, length_scale=100, 'mm.H20', 'kPa')
9.80665
>>> # Demonstrate different ways of specifying units of newtons
>>> froude.dimensions('N')
'L^1 M^1 T^-2'
>>> froude.dimensions('newton')
'L^1 M^1 T^-2'
>>> froude.dimensions('kg.m/s/s')
'L^1 M^1 T^-2'
>>> froude.dimensions('kilogram.metre/second^2')
'L^1 M^1 T^-2'
Froude scaling reference
| Quantity | Dimensions | Scaling exponent |
|---|---|---|
| Length | L^1 | λ^1 |
| Mass | M^1 | λ^3 |
| Time | T^1 | λ^0.5 |
| Velocity | L^1 T^-1 | λ^0.5 |
| Acceleration | L^1 T^-2 | λ^0 |
| Force | L^1 M^1 T^-2 | λ^3 |
| Pressure | L^-1 M^1 T^-2 | λ^1 |
| Overtopping | L^2 T^-1 | λ^1.5 |
Reynolds scaling reference
| Quantity | Dimensions | Scaling exponent |
|---|---|---|
| Length | L^1 | λ^1 |
| Mass | M^1 | λ^3 |
| Time | T^1 | λ^2 |
| Velocity | L^1 T^-1 | λ^-1 |
| Acceleration | L^1 T^-2 | λ^-3 |
| Force | L^1 M^1 T^-2 | λ^0 |
| Pressure | L^-1 M^1 T^-2 | λ^-2 |
| Overtopping | L^2 T^-1 | λ^0 |